채권수익률YTM의 구성요소는 r= r*+IP+RP이다.
여기에서 r은 명목이자율
r* 실질 무위험이자율 - 대부분 국채수익률을 쓰고 어떤 경우는 AAA등급 회사채를 쓰기도 한다.
IP 기대 인플레이션 프리미엄 - 인플레이션은 사후적으로만 측정되기 때문에 '기대'다
RP 위험 프리미엄 - 국채 빼고는 위험이 있다고 본다.
국채 수익률은 여기서 RP 즉, 위험프리미엄이 없다고 보면 되겠지.
여기서 [회사채yield]-[국채yield]의 값을 스프레드 라고 한다.
채권의 가격(채권수익률)은 시장의 수요와 공급에 의해 결정된다.
예를 들어 어떤 회사채의 가격은 거시경제환경(r*,IP)과 회사의 위험도, 그리고 발행조건(약정이자율,만기)등을 반영하여 시장이 결정한다. 그리고 그렇게 가격이 결정되면 채권수익률YTM도 결정되겠지.
채권수익률의 기간구조 / 수익률곡선 Yield Curve
어느 특정시점에서 동일 발행주체가 발행해서 이자율과 신용등급 등 다른 요소들은 같지만 만기만 다른 채권들의 YTM과 만기와의 관계를 그래프로 그려본 것

예를들어 미국국채의 동일한 이자율을 주는데 만기만 다른 국채들을 쫘라락 놔둬보면, 만기가 긴 국채일수록 년 수익률이 높다.
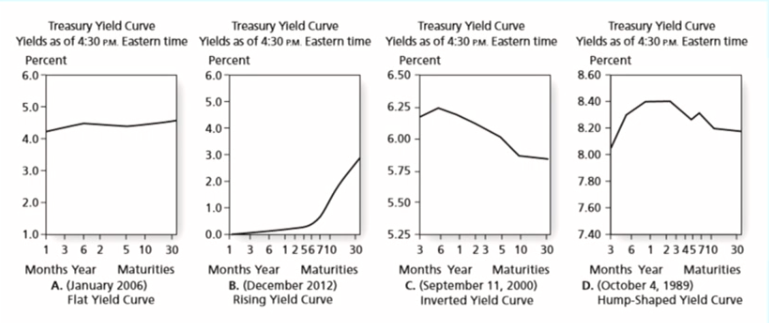
하지만 일드커브는 모두 동일하게 우상향만 하는것이 아니라 다양한 형태를 띈다.
왜 그럴까 알아보자.
그 전에 용어정리 하고 보자.
spot rate : t=0로 현재시점에서 관측된 zero-coupon bond에 대한 YTM
예를들어 Y1이라고 하면 현재시점에서 관측된 만기가 1기간인 zero-coupon bond의 yield다.
short rate : 이론적으로 존재하며, 미래 n-1시점부터 n시점까지의 1기간 이자율
그런데 R1은 Y1과 같으므로 관측된다.
그리고 이거는 불확실성이 없다고 가정한것이다.
하지만 결국 미래는 불확실성이 있으므로 Expected short rate를 사용하게 된다.
forward rate : 실제로 존재하며, 현재시점에서 관측된 미래 기간의 rate로 expected short rate와 다르다.
이건 만기가 다른 spot rates(YTMs)로부터 도출해낸다.
이제 다시 yield curve의 형태가 어떻게 결정되는지 주장하는 세가지 이론을 살펴보자.
(1) 기대가설 Expectations Hypothesis
일드커브의 형태는 시장참가자들이 미래 단기수익률에 대한 기대(expected short rate)에 의해 결정된다.
하지만 여기서는 시장참가자들은 위험중립적이라는 가정이 들어간다. 즉 expected short rate는 forward rate와 같을것이라는 비현실적인 가정을 갖고 가설을 세웠다.
아무튼 요 기대가설에서는 시장참가자들이 미래에 단기이자율 상승을 예측하면 일드커브가 우상향하고 단기이자율 하락을 점치면 일드커브는 우하향한다.
(2) 유동성 선호가설 liquidity preference hypothesis
만기가 긴 채권은 짧은 만기 채권에 비해 투자자들에게 liquidity premium을 통해 더 높은 수익률을 제공해야 한다는 것으로 만기가 길수록 이자율 변동에 따른 채권가격의 변동위험이 크겠지? 그래서 투자자들은 대체적으로 짧은 만기의 채권을 선호하겠지? 그러니께 만기가 긴 채권에는 프리미엄을 줘야한다 이거임.
forward rate = expected short rates + liquidity premium
내 생각에는 이게 맞다.
(3) 시장분할이론 segmented market hypothesis
기관투자자들이 채권시장의 메인플레이어인데 기관투자자들은 영업특성, 관계법규, 만기선호도때문에 만니가 다른 채권으로 쉽게 이동하지 못하는 경직성이 있다. ex) 보험회사는 장기부채관리를 위해 장기채권을 선호, 국민연금은 관계법규 엄격 등등
그래서 기관들의 특성에 따라 장기채권에만 투자하는 새키들도 있고 단기, 중기에만 투자하는 새키들이 있는데 그래서 채권을 장/중/단으로 구분하고 그 안에서 놀기 때문에 yield curve가 요상하게 나온다. (각자의 수요공급에 의해서 그래프가 형성되겠지)
아무튼 요렇게 3가지 가설이 있는데 무엇이 맞는지 정답은 없다고 한다.
자 지금까지 설명, 무슨 개소리인지 모르겠는가?
당신이 옳다.
이런 개같은 이론공부는 도대체 현실에서 쓸모짝이 없다.
이래서 뭐 어쩌라는것인가? 이게 현실에 부합되어 유용하다면 이거 공부 열심히 한 사람들은 다 부자인가?
쓸데없는 탁상공론이다. 쯧쯧
'주식투자 > 투자공부' 카테고리의 다른 글
| 채권공부 (4) 듀레이션의 속성 / 볼록성 / 채권투자전략 (0) | 2020.10.03 |
|---|---|
| 채권공부 (3) 채권가격정리 / 듀레이션 Duration (0) | 2020.10.02 |
| 채권공부 (1) 채권의 가격/ YTM / 재투자위험 / 가격위험 (0) | 2020.09.08 |
| [투자이론] CAPM 자본자산 가격결정모형 / SML, CML 증권시장선, 자본시장선 (6) | 2020.06.25 |
| [금융 공부] CDS, CDO, CLO/ 신용부도스와프, 부채담보부채권, 대출채권담보부증권 (0) | 2020.06.24 |



